- The absolute value of a real number x or the \left| x \right|, is the distance x lies from 0 on a number line.
- The absolute value of a real number is never negative or the \left| x \right|\ge 0
- \left| x \right| =\sqrt { { x }^{ 2 } }
- Piecewise: \left| x \right| =\begin{cases} x,\quad \quad if\quad x\ge 0 \\ -x,\quad if\quad x<0 \end{cases}
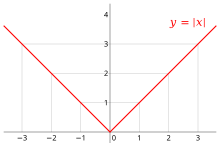
In mathematics, the absolute value or modulus of a real number x, denoted |x|, is the non-negative value of x without regard to its sign. Namely, |x| = x if x is positive, and |x| = −x if x is negative (in which case −x is positive), and |0| = 0. For example, the absolute value of 3 is 3, and the absolute value of −3 is also 3. The absolute value of a number may be thought of as its distance from zero.
Generalisations of the absolute value for real numbers occur in a wide variety of mathematical settings. For example, an absolute value is also defined for the complex numbers, the quaternions, ordered rings, fields and vector spaces. The absolute value is closely related to the notions of magnitude, distance, and norm in various mathematical and physical contexts.

