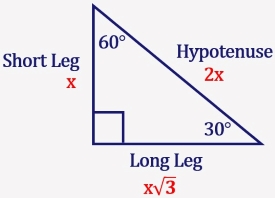
- A triangle with angle degree measures of 30, 60, and 90 is a special right triangle
- Corresponding to opposite angle measures, the ratio of the side lengths of every 30-60-90 triangle is 1:√3:2
- In plain language, the hypotenuse is twice as long as the shortest leg (opposite the 30 degree angle), and the longest leg (opposite the 60 degree angle) is √3 times longer than the shortest leg
- Application: finding the other 2 side lengths of a 30-60-90 triangle given one side length
Position of some special triangles in an Euler diagram of types of triangles, using the definition that isosceles triangles have at least two equal sides, i.e. equilateral triangles are isosceles.
A special right triangle is a right triangle with some regular feature that makes calculations on the triangle easier, or for which simple formulas exist. For example, a right triangle may have angles that form simple relationships, such as 45°–45°–90°. This is called an "angle-based" right triangle. A "side-based" right triangle is one in which the lengths of the sides form ratios of whole numbers, such as 3 : 4 : 5, or of other special numbers such as the golden ratio. Knowing the relationships of the angles or ratios of sides of these special right triangles allows one to quickly calculate various lengths in geometric problems without resorting to more advanced methods.